It’s Just Math
Schools are back in session, and for parents, the tradeoff of having kids at school all day is the added chore of helping kids do their homework at night. When the Yakel kids were in elementary school, it was sort of fun to feel smart helping with 3rd grade spelling or 2nd grade math. But now that our kids range from 5th grade to 10th grade, we are finding it more difficult to help them with their homework – especially the accelerated math courses, like Melanie’s advanced calculus. UGH. Even Ben’s fifth grade long division makes me get a headache.

I DO like math (clearly at sub 5th grade level 🤣)…and at Meridian, we are trying to navigate a basic math problem in the bond market at the moment.
As background, bonds are fixed income investments. When you buy a bond, you are loaning a company money, and they are agreeing to pay it back to you at a certain point in time, with annual interest payments to you along the way. So, a $10,000 Apple bond with a coupon of 5% and a 3 year maturity means that you have loaned Apple $10,000 for them to use to fund their operations. In 3 years, Apple agrees to pay back your principal value of $10,000, and make interest payments of $500/year (usually split into two semi-annual payments) from now until then ($10,000 X 5% annual interest rate=$500):

So, the total value of that bond is just math. The value of the bond is the $10,000 face value plus the total value of the interest payments (6 x $250 = $1,500)…or $11,500.
Every day, new bonds are issued at the going market interest-rate. So, the challenge in a rising interest-rate environment is that if you buy a bond today that offers a 3% interest rate, but tomorrow, new bonds are issued at a 4% interest rate, then your 3% bond does not have the same cash flow that an investor could get from buying a brand-new bond.
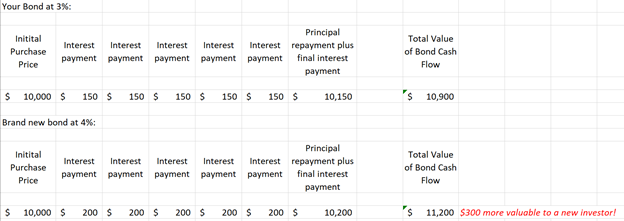
Since you have no control over the interest payments of the bond you own (as those are fixed), the only thing that you can control is the price at which you sell the bond. To make your $10,000 bond that pays 3% interest equal to a new $10,000 bond that pays 4% interest, you have to drop your sale price of your bond down to $9,700, to make it competitive with the new bond issue today:
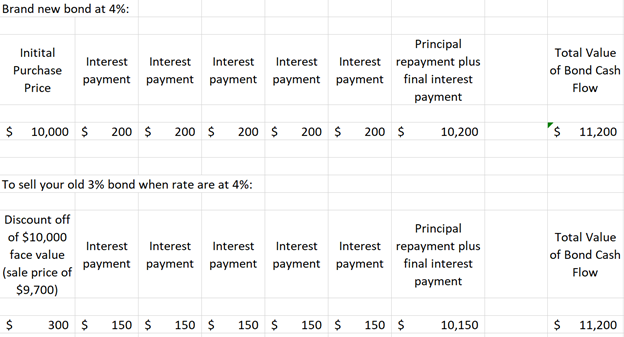
Mathematically, the prices of bonds move inversely to interest rates. So, if interest rates are going up, bond prices will go down.

And that is the current interest rate environment that we find ourselves in at the moment…
With Chairman Powell of the Federal Reserve indicating that they will allow interest rates to rise slightly, bond investors are faced with an environment in which the bonds they buy today will most likely be facing slight price declines as the rates start to rise. This chart from JP Morgan shows the impact of a 1% interest rate rise on existing bonds:
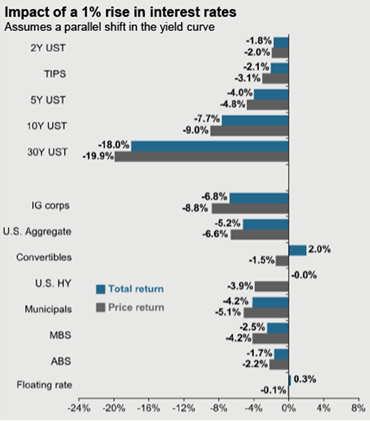
The magnitude of the price decline is related to the length of the maturity of the bond, so you will see longer term bonds are more sensitive to interest rate increases. So, in a rising interest-rate environment, one way to manage interest rate risk is to buy bonds that have shorter maturities. Bonds that are maturing quickly will allow an investor will reinvest the proceeds at the higher prevailing interest rates at the time. Therefore, short term bonds are less impacted by rate increases.
One other way to manage interest rate risk is to invest in a bond mutual fund. These funds own thousands of bonds, and while the prices of the underlying bonds will fluctuate daily with interest rate changes, a bond fund always has bonds that are nearing maturity. With near steady cash flow, a bond mutual fund is able to reinvest the proceeds from maturing bonds into the new bonds that are being issued with higher interest rates:
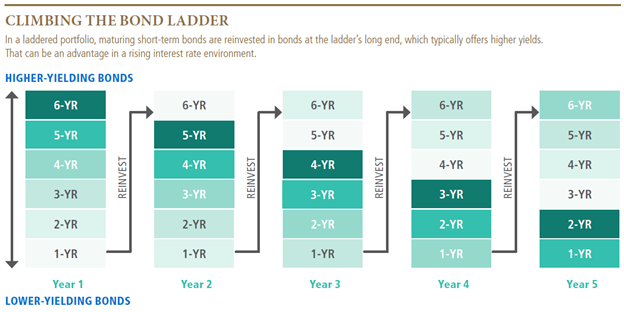
Therefore, bond funds may be able to catch the benefit of the higher interest rates faster than an individual bond.
While bond investors are not accustomed to their fixed income/stable investments facing price declines, when the math behind a bond is understood, the short term losses are to be expected. The challenge for a bond investor in a rising rate environment is to carefully manage the maturity structure of their portfolio, so they are not impacted dramatically by large interest-rate movements!